前言
在金融监管深化与不良资产处置专业化的行业背景下,金融借款合同纠纷批量案件已成为法律服务领域的重要业务方向。此类案件虽具法律关系定型化、诉讼请求标准化特征,但传统单案处理模式面临文书制作效率低下、利息核算逻辑复杂、庭审数据阐释易生歧义等实务难点。基于此,笔者系统研究各类还款方式的利息、罚息、复利算法,形成批量文书自动生成的标准化作业体系。兹就实操经验整理如下,以供业界同仁参考。
本文先解析金融批量案件法律文书自动化生成流程,再重点阐释等额本息还款方式下利息、罚息及复利的精确计算方法。
一、利用“邮件合并”技术实现法律文书批量生成
批量生成法律文书需借助办公软件Word与Excel(或者WPS),其原理是通过主文档与数据源的智能匹配,实现系列文书的批量生成。主文档为各类法律文书的Word模板,数据源系包含被告基本信息、借款要素、欠款数据等变量信息的Excel表格。通过在主文档中插入合并域,办公软件可自动匹配数据源与合并域,生成格式统一但内容各异的法律文书。具体操作分三步骤:
第一步:构建法律文书模板体系
依据案件事实与法律规范,编制起诉状、授权委托书、证据目录、律师函、所函、执行申请书等标准化模板并保存为Word文档。文书模板编制需精益求精,遵循极简原则,仅保留必要法律要素,以减少后续制作数据源表格的工作量。需注意,根据最高人民法院相关指导意见,当前金融借款合同纠纷案件应采用要素式起诉状模板。
第二步:制作标准化数据源表格
法律文书内容可拆解为固定要素与可变要素,其中可变要素主要包括被告姓名、性别、民族、出生日期、公民身份号码、住址等身份信息,诉讼请求中的本金、利息、罚息及复利金额,以及贷款合同编号、签订时间、贷款本金、起息日、贷款到期日、还款数据等案件事实要素。我们需以这些可变要素作为Excel表格的列标题,构建标准化数据源。
在制作Excel数据源表格时,部分数据可直接从金融机构系统导出,故应尽量让客户提供完整的基础数据,剩余数据通过人工录入或数据运算得出。
以下详细说明如何通过已有数据计算所需的关键数据。
1. 基于公民身份号码计算性别与出生日期
根据我国公民身份号码编码规则,18位身份证号码中第17位数字表示性别(奇数为男性,偶数为女性),第7至14位数字表示出生日期。如表1所示,若Excel表格B列第2行单元格B2存储公民身份号码,则可在性别列单元格C2输入函数“=IF(MOD(MID(B2,17,1),2),”男”,”女”)”生成性别信息;在出生日期列单元格D2输入函数“=TEXT(TEXT(MID(B2,7,8),”0000年00月00日”),”YYYY年M月D日”)”生成出生日期信息。读者需注意,实际使用函数时需根据单元格引用位置调整函数参数,下同。
表1 性别、出生日期、管辖法院生成示例

2. 基于被告住址推导管辖法院
若选择在被告住所地法院起诉,可通过被告住址信息以函数运算生成管辖法院。如表1所示,假设Excel表格E列第2行单元格E2存储住址信息,则在管辖法院列单元格F2输入函数“=IFERROR(LEFT(E2,FIND(“省”,E2))&IF(ISNUMBER(FIND(“县”,E2)),MID(E2,FIND(“市”,E2)+1,FIND(“县”,E2)-FIND(“市”,E2)-1)&”县”,MID(E2,FIND(“省”,E2)+1,FIND(“区”,E2)-FIND(“省”,E2)))&”人民法院”,””)”即可生成管辖法院信息。需说明的是,该函数未涵盖户籍地址为直辖市、自治区或县级市等特殊情形,实际应用中可根据需要进一步优化。
3. 精确计算借期利息、逾期罚息及复利
首先,需界定本文涉及的利息概念:狭义利息即“借款期限内利息”(简称“借期利息”),系以未到期贷款本金为基数按照借期利率及借期天数计算的利息,计算公式为:借期利息=贷款本金*借期利率/360*借期天数(借期天数计算采用“含头不含尾”原则,即从贷款本金划付之日起算至贷款到期日的前一日);“逾期罚息”系以到期未付贷款本金(逾期本金)为基数按照逾期利率及逾期天数计算的利息,计算公式为:罚息=逾期本金*逾期利率/360*逾期天数;“复利”系以到期未付借期利息(逾期利息)为基数按照逾期利率及逾期时间计算的利息,计算公式为:复利=逾期利息*逾期利率/360*逾期天数。逾期利率在借期利率水平上加收一定比例,具有违约惩罚性质,即罚息利率。根据《中国人民银行关于人民币存贷款计结息问题的通知》(银发〔2005〕129号)第三条规定,日利率=年利率/360。需特别注意,利息是以未到期本金为基数计算,而罚息是以到期未付本金为基数计算,“未到期”和“到期”是区别利息和罚息的的关键标准。
实际上,“罚息”包括逾期罚息和挪用罚息,鉴于金融借款批量案件中被告挪用借款的举证难度,本文所述罚息特指逾期罚息。
此外,部分金融机构在计算分期还款的复利时,会将上期未还逾期罚息与借期利息合并作为计算基数,因此类做法易被法院理解为“利滚利”而不予支持,本文对此不作讨论。
其次,利息、罚息、复利的计算规则与借款合同约定的还款方式密切相关。金融借款常见还款方式包括到期一次性还本付息、分期付息到期还本、等额本金、等额本息四种。到期一次性还本付息是最常见的还款方式,其利息、罚息、复利计算规则相对简单;而分期付息到期还本、等额本金、等额本息三种分期还款方式的利息、罚息、复利的计算较为复杂,难以通过单一Excel函数实现统一计算,下文在第二部分重点解析。此处先介绍到期一次性还本付息方式下的利息、罚息、复利计算方法。
到期一次性还本付息,顾名思义,是指贷款到期日前借款人无需还本付息,在贷款到期日一次性偿还贷款本金及借期利息的还款方式。若到期日未足额还款,则从当日起开始计算罚息与复利。当然借款人逾期后可能陆续偿还部分本金及利息,每次还款后需重新调整罚息与复利的计算基数,因此需根据还款情况分段计算。举例说明:
假设张三向某银行借款,贷款基本要素如表2所示,要计算借期利息时,可在单元格L2输入函数“=G2*(I2-H2)*J2/360”(借期天数计算遵循“含头不含尾”原则)。
表2 到期一次性还本付息利息算法
张三到期未偿还贷款本息,产生罚息和复利。经过银行催收,张三陆续偿还5次本金,还款数据如表3所示。计算罚息时,可在W2单元格输入函数“=ROUND(SUM(G2*(M2-I2),(G2-N2)*(O2-M2),(G2-N2-P2)*(Q2-O2),(G2-N2-P2-R2)*(S2-Q2),(G2-N2-P2-R2-T2)*(U2-S2),(G2-N2-P2-R2-T2-V2)*(TODAY()-U2))*J2*1.5/360,2)”。罚息利率按借期利率的1.5倍计算,罚息计算至“今天”,若需计算至指定日期,可将函数中的“TODAY()”替换为含指定日期的单元格并设置绝对引用。若还款次数更多,可按此函数逻辑类推。复利计算逻辑与罚息一致,此处不再赘述。
表3 到期一次还本付息法逾期罚息算法
4. 时间、利率、金额等数据的文本格式转换
计算利息、罚息及复利时,日期时间需要使用日期格式,利率需要使用百分比格式,金额需要采用货币或数值格式;而批量生成法律文书时,日期、利率、金额等数据需转换为文本格式。例如,日期在Excel表格中显示为“****年**月**日”,若不转换文本格式,导入word将显示为“****/**/**”。因此,制作数据源表格时需在Excel中额外生成文本格式的时间、利率以及金额等数据。
时间格式转换:若Excel表格D列第2行单元格D2存储合同签订时间,则可在相邻单元格F2输入函数“=TEXT(D2,”YYYY年M月D日”)”;
利率格式转换:若Excel表格L列第2行单元格L2存储借期利率,则可在相邻单元格K2输入函数“=TEXT(L2,”0.00%”)”;
金额格式转换:若Excel表格N列第2行单元格N2存储借期利息,则可在相邻单元格O2输入函数“=TEXT(ROUND(N2,2),”0.00″)”。
以上介绍了制作数据源表格的主要函数,其他函数可根据实际需求自行分析。
第三步:将Excel数据源导入Word模板
批量生成法律文书的难点主要集中在前两步,其中第二步尤为耗时。第三步操作相对简便,第三步操作如下:打开文书模板,依次点击Word菜单栏“邮件”→“选择收件人”→“插入合并域”→“完成并合并”。(见图1)具体步骤为:①点击“邮件→开始邮件合并→普通Word文档”;②点击“选择收件人→使用现有列表”,定位第二步制作的数据源表格;③通过“插入合并域”将变量插入文书模板对应位置;④点击“完成并合并→编辑单个文档→全部”生成文书。需注意,Excel单条记录生成单份文书,多笔借款需人工合并内容。
Word会将Excel中的所有记录生成一个总文档,而WPS可在合并时选择“合并到不同新文档”,并可设置以域名作为新文档文件名,在指定文件夹内生成多份独立Word文件。因此,若需每份文书单独保存,建议使用WPS进行邮件合并。
图1 邮件合并4步骤

二、分期还款方式下的利息、罚息、复利算法
如前所述,分期付息到期还本、等额本金、等额本息均属于分期还款方式,其中等额本息还款方式的利息、罚息、复利计算最为复杂,掌握其规则可贯通其他分期还款方式。以下详解等额本息还款方式的利息算法:
等额本息还款是指借款人按约定周期等额偿还贷款本息。本文以按月还款的等额本息为例进行分析,按季度还款的计算逻辑与此一致。等额本息按月还款中“等额”金额的计算公式源于高中等比数列原理,有兴趣的读者可以查阅公式推导资料。本文直接给出公式:每期应偿还本息合计=贷款本金*贷款月利率*(1+贷款月利率)^贷款期数/((1+贷款月利率)^贷款期数-1)(其中“^”表示乘方运算);每期应偿还利息=贷款余额*贷款月利率(此处贷款余额指贷款本金减去累计应偿还本金后的余额,即未到期本金)。既知每期应偿还本息合计、每期应偿还利息,可得每期应偿还本金=每期应偿还本息合计-每期应偿还利息。
以下通过实例说明如何在Excel中实现等额本息每月还款本息、罚息及复利的计算。
假设张三向某银行借款,贷款基本要素如表4所示,贷款月利率=贷款年利率/12,逾期利率(罚息利率)=贷款年利率*1.5。计算张三每期还款本息合计金额时,可在单元格H2输入函数“=A2*D2/12*(1+D2/12)^F2/(((1+D2/12)^F2)-1)”。注意,后续表5中的函数会引用表4中的单元格数据。
表4 等额本息贷款基本要素

本文等额本息还款默认采用期末还款方式,张三借款日为2024年9月27日,首期还款日为2024年10月26日,首期贷款实际占用天数小于贷款起息日所在月份的自然天数。因此,首期应还利息不适用“每期应偿还利息=贷款余额*贷款月利率”的一般公式,而应按照首期贷款实际占用天数乘以日利率计算,具体为:首期应偿还利息=贷款余额*贷款日利率*首期贷款实际占用天数。首期应还本金仍按一般规则计算,即每期应偿还本金=每期应偿还本息合计-每期应偿还利息=每期应偿还本息合计-贷款余额*贷款月利率。如表5所示,计算第1期应偿还本息时,可在D6单元格中输入函数“=$A$2*$D$2/360*(B6-B2)”,得首期应偿还利息113.42元;在C6单元格输入函数“=H2-$A$2*$D$2/12”,得首期应偿还本金252.24元。计算第2期应偿还本息时,在D7单元格中输入函数“=($A$2-SUM($C$6:C6))*$D$2/12”,得第2期应偿还利息114.64元;在C7单元格输入函数“=$H$2-D7”,得第2期应偿还本金254.93元。后续各期均按此逻辑计算:先算应还利息,再以每期等额还款本息减去应还利息得应还本金。
表5 等额本息贷款利息、罚息、复利计算清单
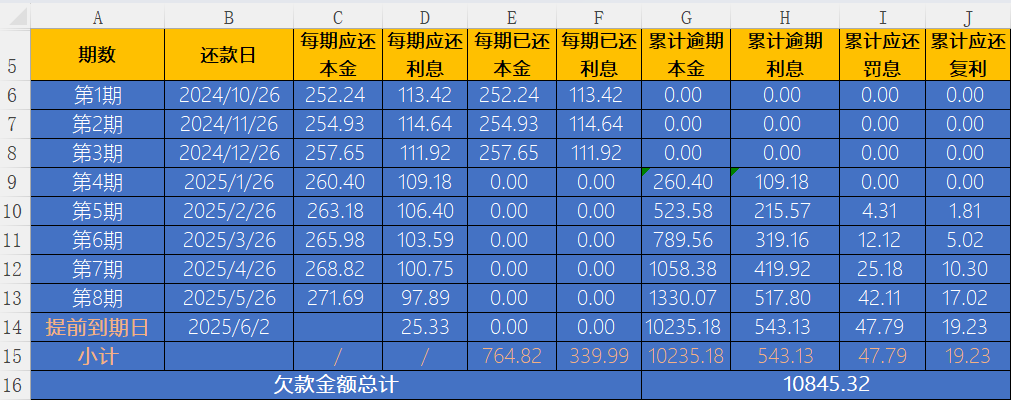
张三在前3期按期足额还款(见表5中E列、F列),从第4期还款日2025年1月16日开始逾期,产生逾期本金和逾期利息。每期逾期本金=每期应偿还本金-每期已还本金,每期逾期利息=每期应偿还利息-每期已还利息(注意表5中的G列和H列是累计逾期本金和累计逾期利息)。而逾期本金和逾期利息分别产生罚息和复利,罚息=逾期本金*逾期利率/360*逾期天数。特别需要注意的是,等额本息分期还款方式下,某期罚息发生额是以上期期末累计逾期本金(即本期期初累计逾期本金)为计算基数。如计算表5中Excel表格I10单元格的罚息时,可输入函数“=G9*$G$2/360*(B10-B9)”,以第4期期末累计逾期本金(G9)为基数计算第5期罚息发生额4.31元,后续各期罚息均按此逻辑计算(表5中I列是累计应还罚息)。复利计算逻辑与罚息相同,此处不再详述。
由于张三逾期时间较长,银行依据合同约定宣布贷款提前到期,提前到期日为2025年6月2日。提前到期日后不再计算正常利息,改为以全部未还本金为基数计算罚息,以全部未还利息为基数计算复利。需注意,计算第8期还款日2025年5月26日至提前到期日2025年6月2日(含当天)的利息时,不适用一般公式,而应按实际占用天数计算,如在表5单元格D14输入函数“=($A$2-SUM($C$6:C13))*$D$2/360*(B14-B13+1)”,即可得相应利息25.33元。
本文在分析等额本息还款的罚息和复利算法时,未考虑借款人偿还罚息和复利的情形。若存在此类还款记录,只需在表5中的Excel表格增加4列,以应还罚息和应还复利分别减去已还罚息和已还复利即可得未还罚息和未还复利。
结语
本文系统介绍了金融借款合同纠纷案件法律文书批量生成技术,并以等额本息为切入点,深度解析利息、罚息、复利算法,期望能对业界同行有所助益。金融借款案件中,欠款金额准确性历来是争议核心,从事金融不良资产诉讼清收业务的律师,应熟练掌握各类还款方式的利息计算规则,避免在庭审中因计算逻辑阐释不清而陷入被动。唯有如此,方能在金融不良资产诉讼清收这一专业领域中赢得客户信任与业界认可。

